2021-04-22

将棋駒の形のデザインができるサイトをもう一度作りました

以前将棋駒の形のデザインができるサイトを作りましたが、あんまりかっこよくなかったり機能も微妙だったのでいつか作りなおしたいなと思っていました。

最近ヒマになったので、Reactという技術を学ぶがてら新たに作成しました。その名も「ショウギゴマデザイン」です。

shogi-piece-design.vercel.app

形をデザインする機能
色をデザインする機能
できた駒画像をダウンロードする機能(ロゴなどに利用できる)
できた駒の座標などの情報をダウンロードする機能(blenderモデルなどに利用できる)

といった機能を有しています。

ショウギゴマデザインのロゴに書いてある将棋の駒も、このショウギゴマデザインで作られています。再帰。

もしよかったら皆さん使ってみて下さい。

2020-11-23

「○○は役に立たない」について

はじめに

インターネットを見ていると、よく「○○は役に立たない」という主張に対して意見の論争がなされている。

私のいる界隈では○○にはkaggleがよく入りがちである。競プロとか、数学とか、博士号なども見かけたことがある。

おそらく、私が知らない界隈では私の知らない単語が○○に入っては論争を巻き起こされているのだろう。

私はこの類の論争は不毛だと思っており、さらにその原因の99％は主張を発言した人の注意が行き届いていないため発生していると考えている。

そこで、この記事では4つの観点から、なぜ論争が沸き起こってしまうのか、どのような主張をしたら論争が沸き起こらないのかについての私見を述べる。

具体的な事例があると良いかと思い、炎上しそうな文章をあまり炎上しない形に変えるチャレンジも併記する。

チャレンジ

以下の文章をあまり炎上しない形に言い換える

kaggleは実務の役に立たない。

なぜなら実務ではkaggleのような状況は起こり得ないからだ。

観点

1. そもそも主張を発言した人が○○を正しく理解していない

議論の前提が間違っていると、当然ながら論争が起こる。

また、○○の界隈にいる人にとっては、正しく理解していないのに適当なことを言わないでほしい、という負の感情が発生するため、争いが白熱しやすい。

主張する対象については正しく理解を行わないといけない。

今回のチャレンジでは、「実務ではkaggleのような状況は起こり得ない」が正しくない。一番典型的なkaggleのタスクである「決まったデータセットに対してモデルを作成して、精度を向上させる」というタスクでさえ、世の中にはそのような仕事があるのは事実だからである。

まず、チャレンジの主張を以下の文章に変えてみる。

kaggleは実務の役に立たない。

なぜなら実務では複数の会社や部署をまたいでプロジェクトを成功させることが求められているからである。

2. ○○のレベル感を記載していない

○○をどれくらいやるのが役に立たない、と記載されていないケースが多いが、これもまた議論の種であると考えている。

「○○は役に立たない」系のほぼすべての主張は、"○○をやり込みすぎても"役に立たない、あるいは"中途半端な覚悟で○○しても"役に立たないという主張であるのではないか。

前者はサッカーに対するリフティング、後者はアイドルに対するボイストレーニングが該当するであろうか。

今回のチャレンジでは、ある程度やったらもう不要だよね、というスタンスで記載してみる。

Kaggle Masterになるレベルでkaggleに力を注いでも、実務の役には立たない。

なぜなら実務では複数の会社や部署をまたいでプロジェクトを成功させることが求められているからである。

機械学習の知識が必要なのはもちろんであるが、Kaggle Masterになるまでやり込む必要はないと考えている。

3. 「役に立たない」対象を明示していない

大体の事象に例外はつきものであり、対象を全人類にして何かが役立つ・役立たないを主張するのはリスキーだと考えている。

誰に対して役立たないのかを明記して対象を絞り込むことによって、炎上のリスクを抑えることができる。

今回のチャレンジの例外は、「複数の組織と関わらない仕事をしている人」「そのようなポジションは他の人に任せ、自分はモデル作成のみを担当する人」あたりであろうか。

これを踏まえて、以下のように文章を変えてみる。

大企業の中でAIプロジェクトを推進していくポジションの人間にとって、

Kaggle Masterになるレベルでkaggleに力を注いでも、実務の役には立たない。

なぜなら実務では複数の会社や部署をまたいでプロジェクトを成功させることが求められているからである。

機械学習の知識が必要なのはもちろんであるが、Kaggle Masterになるまでやり込む必要はないと考えている。

4. 「役に立たない」のレベル感のすり合わせができていない

個人的には、私はあらゆる行為があらゆる行為の役に立つと考えている。

例えば、私は地下アイドルオタクを昔やっていたが、この経験は非常に機械学習エンジニアとしての活動に役立っていると思っている。

これはビジネスモデル、オタクやアイドルの心理、小数チームのマネジメント、toC向けビジネスの炎上ポイントなどを知ることができたからである。

しかし、地下アイドルオタクをするだけではもちろん機械学習エンジニアにはなれないし、しなくてもなれる。

このレベルの「役に立つ」を「役に立たない」と判断する人も多いであろうことは容易に想像がつく。ここのすり合わせができていないことが無駄な論争に繋がっていると考えている。

今回のチャレンジでは、kaggleが"複数の会社や部署をまたいでプロジェクトを成功させること"に役立たないという主張をする。

しかし、kaggleにはチームマージというシステムが存在する。このチームマージが"複数の会社や部署をまたいでプロジェクトを成功させること"の役に立つと考える人もいるかもしれない。

そこで、以下のように「役に立つ」のレベル感を追記してみる。これがこのチャレンジの終着点である。

大企業の中でAIプロジェクトを推進していくポジションの人間にとって、

Kaggle Masterになるレベルでkaggleに力を注いでも、実務の役には立たない。

なぜなら実務では複数の会社や部署をまたいでプロジェクトを成功させることが求められているからである。

確かにチームマージやホストとのやりとりという面でコミュニケーション力が鍛えられることは間違いないが、そのレベルの経験だとあと一歩足りないというのが実感である。

その理由は、kaggleに関わっている人はみな機械学習の導入に前向きだからである。機械学習の導入に前向きでない人を巻き込む経験がないと、役に立つとは言えないと考えている。

機械学習の知識が必要なのはもちろんだが、Kaggle Masterになるまでやり込む必要はないのではないか。

終わりに

このあたりまで気をつけて書けば、少なくとも互いを尊重した議論ができるのではないか。

ちなみに、今私はかなり納期に追われていて、現実逃避のためにこのブログを書いている。

ブログ執筆は納品の役に立たない。

2020-08-22

TensorFlowのSavedModelの便利さを紹介する

はじめに

今は2020年8月なのですが、コロナ禍だし、暑いし、経済状況最悪で暇だし、良いことないですね。

暇になったので、1年ぶりにkaggleをやってみました。

Landmark Retrievalという建物の画像検索コンペに出たところ、そのコンペの提出形式がTensorFlowのSavedModel形式でした。

私はTensorFlow案件をけっこうやってきたので抵抗はなかったのですが、この制約が原因となったのか、あまりこのコンペの参加者は多くなかったようです。

kaggleの提出形式としては賛否両論あると思いますが、実務ではとても便利な形式だと私は思っています。

それなのにもし実務でも敬遠されているとしたらもったいないと思い、この記事ではSavedModelの便利さについて紹介してみます。

ちゃんとした使い方は公式リファレンスを当たってもらうとして、概念やsaved_model_cliの活用方法をお伝えするのを主眼に置いています。

このモデルに画像を入力するとエラーが出ちゃったんだけどどうすればいいの？入力サイズを教えて？あ、あとフォーマットはuint8でいいんだっけ？
今設計を考えているんだけど、このSavedModelの出力ってどういう形式なんだっけ？

これに毎回回答するのも大変だし、モデルのreadmeに毎回過不足なく必要な情報を残しておくのを人力に頼ると記入漏れなどのミスが起きそうで嫌ですよね。

そんなときに便利なのがsaved_model_cliです。

saved_model_cliについて

saved_model_cliとは、TensorFlowが公式でサポートしている、SavedModelの中身をチェックするためのcliツールです。

TensorFlowをインストールする際に自動でついてきているので、実はTensorFlowが入っている環境下であればすぐに使うことができます。

色々使い方はあるのですが、最も単純な使い方だけ説明します。

saved_model_cli show --dir <SavedModelのパス> --all

とコマンドを打つと、以下のようなモデルについての情報が出力されます。(これは前述kaggleコンペの私のモデルの情報です)

signature_def['serving_default']:
  The given SavedModel SignatureDef contains the following input(s):
    inputs['ts_image'] tensor_info:
        dtype: DT_UINT8
        shape: (-1, -1, 3)
        name: serving_default_ts_image:0
  The given SavedModel SignatureDef contains the following output(s):
    outputs['global_descriptor'] tensor_info:
        dtype: DT_FLOAT
        shape: (1536)
        name: StatefulPartitionedCall:0
  Method name is: tensorflow/serving/predict
…

これにより、以下のような情報がわかります。

入力
- 入力はひとつ
- 入力画像のshapeが(-1, -1, 3)
- データ型はuint8
出力
- 出力もひとつ
- 出力ベクトルのshapeが(1536)
- データ型はfloat

メリット

イントロの気持ちに戻ってみてください。

他のエンジニアからモデルについての質問が多く、生産性が下がっている状態です。

そんな時は、モデルについての情報を毎回他のエンジニアに伝えるのではなく、saved_model_cliの存在を教えて、「その情報はsaved_model_cliを叩けばわかりますよ」と返すのはいかがでしょうか。

私は前の現場でそのような形でsaved_model_cliを広めまくっていたのですが、段々と浸透してくると不要なやり取りが減り、組織としてハッピーになったと思っています。

この生産性向上が最大のメリットと感じています。

また、readmeを毎回モデル作成時に書く運用でも理論上はOKなのですが、readmeを更新し忘れてしまうとモデルの説明とモデルに齟齬が生まれ、余計なコストがかかってしまいます。

簡単に・確実にモデルの中身をチェックできるという意味でも、SavedModel + saved_model_cliのメリットは大きいです。

TensorFlow Servingで簡単にデプロイできる

TensorFlow Servingとは、SavedModelを指定して起動するとそのモデルをAPI化してくれるシステムです。

以下のような特長があります。

パフォーマンスが優れている
http / grpc両対応
モデルのバージョニングができる

このTensorFlow Servingを活用することにより、SavedModelを簡単にデプロイすることができます。

SavedModel + TensorFlow Servingで手軽に高機能のデプロイが実現できるところも、また大きなメリットと感じています。

SavedModel使い方リンク集

ここまでで世の中にまとまっていない情報は大体書ききったので、後は先人の記事に任せてみます。

official

Using the SavedModel format | TensorFlow Core

Serving a TensorFlow Model | TFX

unofficial

SavedModelについてのまとめ - Qiita

TensorFlow2.0時代のTensorFlow Serving向けモデル出力 | AI tech studio

TensorFlow Servingで機械学習モデルをプロダクション環境で運用する - freee Developers Blog

おわりに

ここまで紹介したように、SavedModelはかなり運用に向いている形式であると感じています。

TensorFlowで学習したモデルをデプロイする時は、有力な選択肢として考えるとよいのではないかと思います。

余談ですが、TensorFlow-SavedModel-Tensorflow Servingの関係は、PyTorch-ONNX-ONNX Runtime Serverの関係と似ています。

個人的にモデル作成しやすいのはPyTorchなのでこちらも魅力的に思っています。

しかし、Tensorflow→SavedModelの変換は(個人的な経験では)100%成功するのに対し、PyTorch→ONNXの変換はまだ完全にうまくは行かないという認識です。

そのためモデルの精度要件が緩めで運用の要件が厳しめだったらTensorFlowを採用するのもアリかな、と思っています。

ここらへんの私の考えに甘さがある場合、コメントにてご指摘いただければ嬉しいです。以上です。

2020-05-17

将棋駒の形のデザインができるサイトを作りました

はじめに

2021.04.22追記：さらに高機能なものを作りました。こちらをおすすめします。

rskmoi.hatenablog.com

以前、以下のようなブログを書きました。

rskmoi.hatenablog.com

最近、この記事へのアクセスが伸びています。コロナウイルスによる外出自粛にともない、将棋の駒を作りたい方が増えているのでしょうか。

そして、この記事の一番下にはこう書いてあります。

計算用スクリプトは近日中に公開するので、だれでも将棋駒の辺の長さを知ることができるようになります。

2年経った今も公開していないのは最高に悪質ですよね。そこで、グラフィカルに将棋の駒の形を確認しながら各種の計算ができるサイトを作りました。

その紹介用の記事です。

サイトについて

以下のサイトです。

https://rskmoi.github.io/shogi_piece_web/#/

イメージはこんな感じです。

f:id:rskmoi:20200517172732p:plain — イメージ

使い方は簡単。スライドバーでそれぞれのパラメータの値をいじると、将棋の駒の形が変化していきます。良い形だと思ったらCopy to Clipboardでコピーをするだけです。

あとはその値をblenderで使用する、あるいは木材にプロットするなどお好きなように使用して下さい。

技術力が低すぎてスマホ対応ができていません。スマホから見る場合は横にするとなんとかなります。すみません。

サイトの技術について

このサイトはFlutter for Webでできています。

フロントエンドを全く通ってこなかった人間にとって、プロトレベルであればサクッとwebサイトを作れるFlutterはとても使いやすいです。

終わりに

近日中にスクリプトを公開すると言いながら2年以上放置するというカイジに出てくる悪い人みたいなことをしてしまいましたが、もし活用いただけたら嬉しいです。

あとやっぱりフロントエンドができないと価値を多くの人に届けられないなーと思いました。全部1人でやるなら勉強しないといけないなと思いましたが、人間のリソースは有限なので、難しいですね。以上です。

2019-12-20

画像系機械学習プロダクトで手元のスクリプトとデプロイ環境の精度が違うときのチェックリスト

はじめに

みなさんこんにちは、いかがお過ごしでしょうか。

機械学習もだいぶ広まってきて、右も左も無限に強い人ばかりで、はやく3億円稼いですべてから解放されて虹コン大好きクラブとして生きていきたい今日この頃です。

機械学習がだいぶ広まってくると、機械学習モデルをデプロイする人も増えてきていると思います。

しかし、機械学習モデルのデプロイは非常に複雑です。

モデル、依存ファイル、前処理/後処理、ライブラリ、その他を実験スクリプトと揃えながら、リクエストに対してレスポンスを返すサーバーを継続して稼働させる必要があるためです。

さらには複数人で開発する場合、コードすべてを把握することが難しい、といった困難も付随します。

すると当然、「手元で出ていた精度と、デプロイ環境にリクエストを投げたときの精度が違う」といったバグが生じます。

本日は、そんなときにバグ原因を見つける方針を記事にしたいと思います。

なぜなら、今日まさにこのバグ発見作業で半日溶かしたからです。

それなりに機械学習と触れ合ってきた私でも苦しんだので、チェックリスト的なものがあると便利かと思いました。

もっとよい方法があったり間違ったことを言っていたらコメントで教えてください。

状況の前提

機械学習モデルを作ったり、その精度を測るスクリプトが手元にある
- 対象のモデルは画像系で、Deep Learningを用いている。
上記スクリプトを用いて作ったモデルが内蔵された、HTTPリクエストなどを受け付けて、推論結果をレスポンスで返すサーバがある
その2つに同じ画像を投げているのに、返ってくる結果が違うので困っている

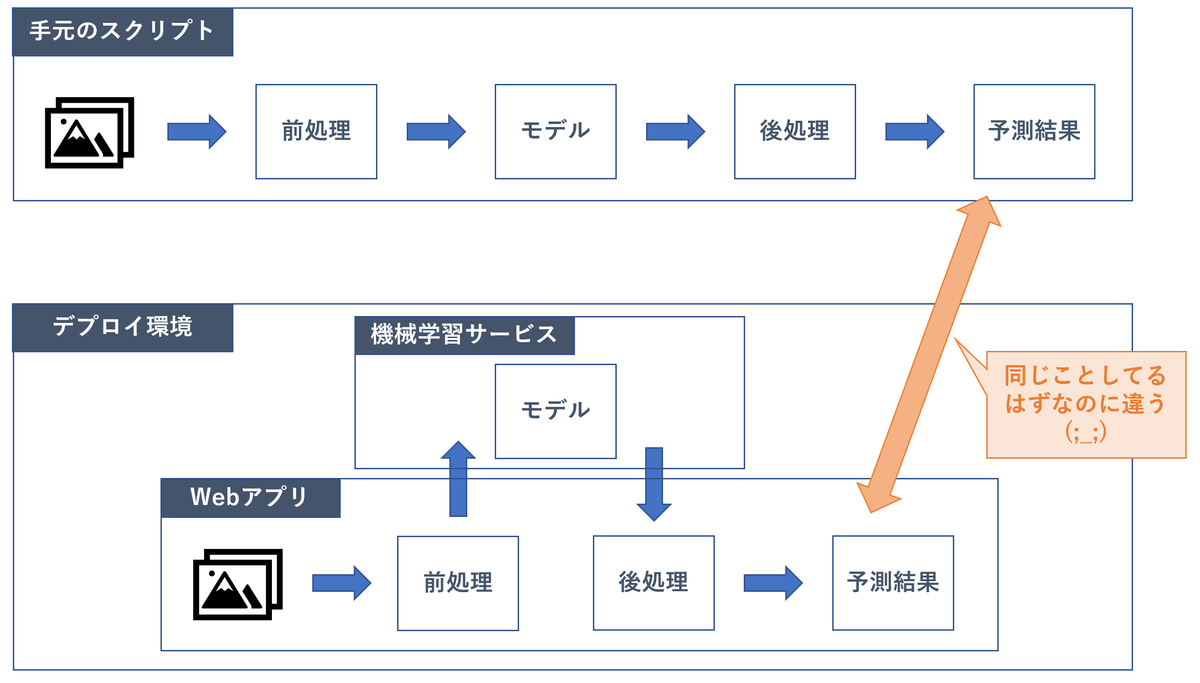
チェックリスト

そもそも本当に同じ状態で精度計測しているかの確認

モデルが同一であるか確認する

モデルが違うと、当然出力も異なります。そのため、まずはここから疑うのがよいと考えています。

デプロイ環境で参照しているモデルを手元に落としてきて確認するのが最速かと思います。

ここで、onnxやtensorflowのsaved modelのような、ネットワーク定義とモデルパラメータがセットで保存されるような形式を使用しているとかなりデバッグがはやくなります。

入力画像が同一であるか確認する

全然違う画像を推論させていると当然全然違う結果になりますが、この辺を疑うことから始めておくと悲しみが防げるかと思います。

画像が同一であるかを簡易的にチェックするためには、hashlibを使うことが多いです。適当にprintして、一致しているかどうかを目視確認、くらいでいいかと思います。

例えばこんな感じで。

from PIL import Image
import numpy as np
import hashlib

def get_hash(image_path):
    image_array = np.asarray(Image.open(image_path))
    hash = hashlib.sha256(image_array.tostring()).hexdigest()
    return hash

依存ファイルが同一であるか確認する

「依存ファイル」の表現は広いのですが、例えばクラスのindexとクラス名のマッピングを記述したファイルなどが挙げられます。

(index0が犬でindex1が猫で、、のようなファイル)

このあたりもチェックするとよいと考えています。

そもそも推論に再現性があるのかの確認

手元の推論を複数回行ってみる

たまに盲点になるのですが、何らかのランダム要素が入って再現性が無いケースがたまにあります。

モデルに入るまでの確認

HTTPリクエストのときに圧縮したりしていないか

JPEGは非可逆圧縮のため、リクエストにJPEG形式を用いていると画素値が微妙に異なってしまうことがあります。

これもhashで確認してみましょう。

前処理が同一であるか

通常、生画像をそのままネットワークに入力することはありません。

正方形になるようにリサイズ / padding
255で割ったり平均を引いたりして正規化

のような操作をした後、ネットワークに入力します。

この処理に違いがあると当然異なる結果になるので、確認します。

処理を追うのも良いですが、最も簡単なのはネットワークに入る直前の画像のhashを比較することです。

hashが違ったら、前処理のどこが違うのかをチェックします。観点として抜けやすいのは以下辺りでしょうか。

処理の順番
リサイズのアルゴリズム

モデルを出てからの確認

モデルの出力が同一であるか

出力のshape
出力のlogit値

などをプリントして確認します。

後処理が同一であるか

前処理同様に後処理についてもチェックします。

モデル内部の挙動の確認

上記に従って後処理まで追うと、

バグ原因がわかった！
モデル内部に謎のバグ原因がある...

のどちらかになるのではないかと思います。モデル内部をもうちょっと頑張って見てみましょう。

trainingモードで推論していないかチェック

手元かデプロイ先のどちらかで、推論時にtrainingモードを用いていないかチェックしてみて下さい。特に推論用にexportされた形式を取っていない場合に起きやすいかと思います。 pytorchだと、trainingモードかevalモードかをmodel.eval()などで設定します。

pytorch.org

具体的には、trainingモードとevalモードだと一般に以下のような違いがあります。(フレームワーク毎に色々あるかもしれないので適宜調査してみて下さい。)

batch normalization: training時はミニバッチの平均や分散を用い、eval時はtraining時に計算された移動平均の値を用いる
dropout: training時は確率的にdropoutし、eval時はしない

バッチサイズを変えて出力をチェック

↑のbatch normalizationもそうですが、バッチサイズによって出力が異なるかどうか確認するのもよいかと思います。

本日の私のケースは少々特殊なケースであったため、この推論時のバッチサイズが手元とデプロイ先で異なることに起因して、片方で潜在的なバグが発動していたケースでした。

ライブラリやデバイス等のチェック

ライブラリのバージョンやデバイス(CPU/GPUなど)による差異を確認することで解決するケースもあるかと思います。

上記をやって、それでもだめだったら

ごめんなさい。遭遇/解決したらコメントで教えて頂けると嬉しいです。

おわりに

以上です。色々な機械学習プロダクトをPoCで終わらせずに運用まで持っていって、こういう知見をつけまくって、実務グランドマスターになりたいですね。それでは。

2019-03-22

Kaggle VSB Power Line Fault Detection (電線コンペ)スコア推移晒し

概要

VSB Power Line Fault Detection | Kaggle に参加して、Public120→Private346位でした。
Public LBに過適合してしまった人間のスコア推移をご覧ください
- Public LBも大したことはなくてむしろshake upを狙っていたのですが…
なかなかひとりの人間の２カ月のスコア推移をみることはないと思うので共有します
- この記事を読んでも機械学習的な学びはほぼないです

スコア推移

f:id:rskmoi:20190322221943p:plain

縦軸がスコア、横軸が時系列です。
赤がPublic, 青がPrivateなので、時間をかけて最終評価スコアを悪化させていることがよくわかります
なんか色がついている背景はprivateでの金/銀/銅圏を表しています

詳細

f:id:rskmoi:20190322222846p:plain

最序盤は画像認識エンジニアらしくグラフを画像化して2DCNNやってたんでひどいスコアです
LSTMは基本的にPublic KernelをPyTorch実装して手を加えてました。以下を変えながらいろいろやってました
- ネットワーク
- 特徴量
- Denoising
論文はhttps://arxiv.org/pdf/1801.04503v1.pdfを参考にしました
seed averagingを50モデルでやってたのでめっちゃモデルの再現性ありました
- これでガチャには勝てると踏んでいたのですがそういう問題じゃありませんでした
「終わりの始まり」でだいたいのベースラインモデルが決まったな～という気持ちに勝手になっていました
- ここまでのモデル微修正の過程が全部Publicにしか効かないやつだったのでしょう
- 一回モデル作ったらチューニングは３回までとか誰か強いグラマスが言ってた気がするし、ちゃんと従ったほうがよかったかもしれません
最終submitはQuoraの3位のモデル(3rd place kernel | Kaggle)にaugmentationとweight decayを加えて汎化性能バキバキに上げたつもりのモデルを採用しました
- Denoisingなし

最後に

こんな感じのスコア推移でした。反面教師として活用してください(?)
どうやってPrivate がいいやつを選べたかはまだわかっていません。落ち着いたら向き合ってみます。
なにより、きちんと狙って上位をとっている方が多数いるようなので、謙虚に学ばなければという気持ちでいます。また頑張ります。

2019-03-15

水沢心愛さんから学ぶ会議の極意

はじめに

今この記事を読んでいる皆様を含む日本人の多くが「会議」という行為を日々行っています。

しかしながら、会議をうまく行うのは非常に難しいです。会議とはこうあるべき！と思っていてもついつい以下のような会議にしてしまうことがあります。

3時間の会議だったのに議事録にまとめたら5行だった
途中からみんなが何を話しているのかよくわからなくなって今日食べる晩御飯のことばかり考えている
会議が終わる理由が「時間が来たから」である

私もまだまだ未熟で失敗することも多いですが、そんなとき私はこの動画を見て、会議とはこうあるべきだと意識を引き締めなおしています。それがこちらです。

ベボガ!新自己紹介会議　[ベボガ!(虹のコンキスタドール黄組) ]

ベボガというアイドルが新しい自己紹介フレーズを決める動画です。(残念ながら2018年に解散してしまっています)

もっと上手く会議がしたいと思っているあなた、特にアイドルの動画紹介なんてくだらないネタブログだと思ったそこのあなたに、是非この動画の真髄を解説したいと思いこの記事を作成しました。

概要

ベボガ!という(既に解散してしまった)アイドルのとある動画を軸に、会議とはこうあるべきだよね、という解説をする記事です
特にリーダーの水沢心愛さんに焦点を当てて書いています
以下を気をつけると短くて意思決定がスムーズないい会議になりますよね、というお話です
- 最初に会議の目的を言う
- 事前に意思決定用の資料を用意する
- アイデアを出しやすい空気を作る
- 簡潔にまとめるリーダー的存在をつくる
- 最後におさらいをする

会議に大切な要素を水沢心愛さんから学ぶ

私が冒頭で紹介したYoutube動画は、ベボガ!というアイドルが、6人それぞれの新しい自己紹介フレーズを決める、という会議の模様を収録したVTRです。

動画の長さは(もちろん編集済みですが)8分と短いのに、素晴らしい自己紹介をバシバシ決めていきます。痛快です。

いい会議とは、こういった「短いのに、素晴らしい意思決定が次々とされていく」会議のことではないでしょうか。

この動画は、特に水沢心愛さんという右奥に座っているアイドルを中心に会議が回っていきます。私はこの動画から、会議に大切な5つのことを水沢心愛さんに教わっている気がしてならないのです。

その5つとは

最初に会議の目的を言う
事前に意思決定用の資料を共有する
アイデアを出しやすい空気を作る
簡潔にまとめるリーダー的存在をつくる
最後におさらいをする

ではないかと考えています。ひとつずつ見ていきましょう。

最初に会議の目的を言う

動画を再生してください。開始0〜6秒で水沢心愛さんは「はい、今日はべボガのね、自己紹介を変えるべく会議をしたいと思います！」と発言しています。

こんなに素早く目的から入る会議を皆さん体験したことがありますか？ここに水沢心愛さんの素晴らしさがあります。

意思決定のための会議では、「この会議で何を決定するか」を最初に提示することが何より大切です。このことにより、会議に参加している人全員が集中して意思決定をすることができます。

これが自然とできている水沢心愛さんは普通のサラリーマンのレベルを大きく超えています。

事前に意思決定用の資料を共有する

続いて、開始12秒で事前にファンに対しtwitterでキーワードを募集している旨が明かされます。

これもまた、会議の開催にあたり非常に素晴らしい姿勢です。

意思決定に当たって、何を基準にするかというのは意外と決めづらいものです。また、制約が少なければ少ないほど議論は発散しがちです。

そこで、事前にこの資料に従って決めるというビジョンをメンバーに共有しておくことで会議の進行をスムーズにしています。

実際、Twitterコメントを軸に6名中4名の自己紹介が決定しています。

アイデアを出しやすい空気を作る

水沢心愛さんは、教科書的な会議進行だけでなく、コミュニケーションスキルにも長けています。

その1 最初の雰囲気作り

開始30秒から、水沢心愛さんはまず最初に自分の自己紹介を決めています。

最初は少し固い空気に見えなくもないのですが、水沢心愛さんは「自称センター」自虐をすることで空気を和らげて、進行役に何を言ってもよいのだという空気を作り上げています。

最初にこのような発言しやすい雰囲気を作ることで、よりよいアイデアが生まれやすい状態になっています。

「ザ・有能」っぽい人ほどこのようなプレイイングはできないものです。我々サラリーマンが見習うべき姿勢ではないでしょうか。

その2 意見を褒める

明らかに水沢心愛さんのセンスが飛び抜けていますが、それでも水沢心愛さんは他のメンバーの意見を褒めることでよりメンバーの発言をより活発にしています。

例えば3:19では葉月梨花さんの意見に対し「いいじゃん」と肯定の言葉を投げかけています。するとそのすぐ後に葉月梨花さんは「『いませんか〜？』みたいなのやりたいかも」とさらなる良いアイデアを出してくれました。

このアイデアが結果的に自己紹介に採用されています。発言者を肯定することでいいアイデアが出てくる貴重なサンプルを水沢心愛さんはいとも簡単に作り上げてしまうのです。

簡潔にまとめるリーダー的存在をつくる

水沢心愛さんは、意見をまとめることにも長けています。

6人の自己紹介が決定する直前の様子を見てみてください。なんと、6名中5名が、水沢心愛さんのまとめで自己紹介が決まっているのです。

意見を出すことと、意見をまとめることはまた別のスキルであるように思います。そして、意見を出す人は上手く意見をまとめてくれる人がいるからこそ安心して発言できるのです。

この役割をこなせるかどうかはある程度センスにも依存するので、進行役の水沢心愛さんがやらなくてもいいポジションであるとは思います。しかし、水沢心愛さんは天才なのでこの立ち回りもできてしまうのです。

最後におさらいをする

7:30から、水沢心愛さんは「はい、べボガの自己紹介が決まりました」と発言しています。

何気ない一言にも思えますが、これもまた重要なことです。

最初に発言した会議の目的に対するアンサーが最後のおさらいになっているかを改めて確認することで、本当に正しく会議ができたのかの確認ができます。

最初の発言を覚えていますか？

「はい、今日はべボガのね、自己紹介を変えるべく会議をしたいと思います！」

でした。

それに対して、

「はい、べボガの自己紹介が決まりました」

でまとめています。完璧ですね。最高の会議です。

終わりに

ここまで見てきたように、この記事で紹介している動画にはいい会議への素晴らしいエッセンスがたくさん詰まっています。

普通のサラリーマンが素晴らしい会議をするのを見るよりアイドルが素晴らしい会議をするのを見るほうが精神的負荷も低いので、みなさんも是非この会議動画をバイブルにしてみてはいかがでしょうか。

ちなみに、水沢心愛さんはベボガ!解散後に沖縄でタピオカ屋さんのオーナーをしているそうです。これだけの会議ができるからこそオーナー業という新しい分野にチャレンジできるのでしょうね。本当に能力が高く、尊敬できる方だと思います。

mdpr.jp

今後も末永く応援していきたいと思っています。

はじめに

チャレンジ

観点

1. そもそも主張を発言した人が○○を正しく理解していない

2. ○○のレベル感を記載していない

3. 「役に立たない」対象を明示していない

4. 「役に立たない」のレベル感のすり合わせができていない

終わりに

はじめに

目次

SavedModelとは

SavedModelの何が便利なのか

学習環境と推論環境でのソースコードの二重管理が防げる

saved_model_cliを活用することで、ネットワークのin/outを楽に・確実に確認することができる

イントロ

saved_model_cliについて

メリット

TensorFlow Servingで簡単にデプロイできる

SavedModel使い方リンク集

unofficial

おわりに

はじめに

サイトについて

サイトの技術について

終わりに

はじめに

状況の前提

チェックリスト

そもそも本当に同じ状態で精度計測しているかの確認

モデルが同一であるか確認する

入力画像が同一であるか確認する

依存ファイルが同一であるか確認する

そもそも推論に再現性があるのかの確認

手元の推論を複数回行ってみる

モデルに入るまでの確認

HTTPリクエストのときに圧縮したりしていないか

前処理が同一であるか

モデルを出てからの確認

モデルの出力が同一であるか

後処理が同一であるか

モデル内部の挙動の確認

trainingモードで推論していないかチェック

バッチサイズを変えて出力をチェック

ライブラリやデバイス等のチェック

上記をやって、それでもだめだったら

おわりに

概要

スコア推移

詳細

最後に

はじめに

概要

会議に大切な要素を水沢心愛さんから学ぶ

最初に会議の目的を言う

事前に意思決定用の資料を共有する

アイデアを出しやすい空気を作る

その1 最初の雰囲気作り

その2 意見を褒める

簡潔にまとめるリーダー的存在をつくる

最後におさらいをする

終わりに