姓名分割プログラムをつくる-手法編-
(201701/23追記)
この記事にミスが見つかりましたので是非とも訂正編もあわせてご覧になってください。すみません。
人間だれでも一度は姓名分割を自動化したくなったことがありますよね?
しかしながらネットにはほんの少ししか姓名分割にチャレンジしている人がいないのが現状です。
精度もあまり高くありません。
ということで自分で姓名分割プログラムを作ってみました。
まあまあうまくいったのでブログにする次第です。
試行錯誤はけっこうしたのですが、内容がぶれるのを恐れてあくまで手法の解説記事とします。
要件
入力:篠田麻里子 出力:篠田 麻里子
のようなプログラムを作る
ざっくりした方針
さて、まず絶対にやりたくなかったのが苗字・名前データベースの作成です。理由は以下です。
・どれだけ苗字を用意すればいいのかわからない
・森、森久、森久保など苗字がどこまでなのかの判定が難しそうだったから(データ数的に)
というわけで漢字一文字ベースで判定をする方針にしてみました。
名前を区切れる場所すべてで区切っていき、
この漢字(一文字)は名前にあることが多いのか苗字にあることが多いのか、、といった確率を最大化する姓名分割方法を探す、というのが方針です。
- 大量の名前データ(以下、漢字学習データ)を準備する
- 漢字学習データから漢字とその出現データをまとめたリストをつくる
- 作ったリストをもちいて名前に対し特徴量を作成する
- 特徴量を用いて正しい場所で区切れているかそうでないかロジスティック回帰を行う
- テストデータで評価
というステップでモデルの作成をしました。
手法
漢字学習データを準備する
無作為に取ってきた人名34642人分を使いました。
ここでいう無作為とはこの苗字が欲しい!という取り方ではなく、ある業界(たとえば「バレーボール選手」など)から取得できるだけの人名を取得するということです。
wikiからなるべく男女比が1:1になるように様々な業界の名前を取ってきたりしました。
けっこう姓名分離されているケースが少なかったので頑張って自分で姓名を分離しました。辛かった。
プロゴルファーと日本証券アナリスト協会の名簿がネットに転がっていたのが本当に助かりました。
漢字学習データから漢字とその出現データをまとめたリストをつくる
漢字一文字を以下のようなデータ構造で保管します。(例は「田」)
田,690,57,4386,0,2,0,2,4911,220,0,0,0,1,1
意味は以下のようになります。
[漢字]
文字:田
[出てくる場所についての情報]
苗字一文字目の観測数:690
苗字その他文字目の観測数:57
苗字最後文字目の観測数:4386
名前一文字目の観測数:0
名前その他文字目の観測数:2
名前最後文字目の観測数:0
[長さについての情報]
この漢字が含まれる苗字の長さが1の観測数:2
この漢字が含まれる苗字の長さが2の観測数:4911
この漢字が含まれる苗字の長さが3の観測数:220
この漢字が含まれる苗字の長さが4以上の観測数:0
この漢字が含まれる名前の長さが1の観測数:0
この漢字が含まれる名前の長さが2の観測数:0
この漢字が含まれる名前の長さが3の観測数:1
この漢字が含まれる名前の長さが4以上の観測数:1
観測数が10回以上のものを漢字リストに入れる条件としたところ、744種類の漢字データが集まりました。
なんでこの構造にしたかは次の項で。
作ったリストをもちいて名前に対し特徴量を作成する
特徴量は2つ、OrderPointとLengthPointです。
定義
OrderPoint
n文字からなる名前があったとします(n > 1)
[出てくる場所についての情報]データをもとに、i番目の漢字に対して
を求めます。
ただし、i ≠1,nです(1文字目が苗字の一文字目なのもn文字目が名前の最後文字目なのも確定だから)
篠田 麻里子の「里」で例示すると、
里,12,1,38,46,48,78,2,40,9,0,0,95,77,0
とあるので
といったところです。
最後に
としてOrderpointを求めます。
LengthPoint
n文字からなる名前があったとします(n > 1)
[長さについての情報]データをもとに、i番目の漢字に対して
を求めます。
最後に
としてOrderpointを求めます。
なんでnではなくn-1で割っているかみなさんはわかりますか?
なんと私もわかりません。nで割るべきでしょう(ブログを書いていて気付いた)
(2017/01/23追記)
やっぱりただのバグでした。以下の情報は参考程度に読んでください。。
しかしnで割ったほうが精度が出ません。つらい。
nが小さいほどLengthPointの重要性が高まることをうまく表現しているととらえてお茶を濁しましょうかね。つらい。
説明
これは我々人間が苗字と名前の分割をこの2つでやっているのではないかという仮説の元作成した特徴量です。
・OrderPointについて
篠田麻里子が篠田 麻里子とわかるのは、
「麻」が名前の1文字目にある可能性が苗字の最後にある可能性より高いからそう判断しているのではないでしょうか?
篠田川里子さんだったら篠田川 里子と分割する人が多いように思います。
という考えをモデル化したものです。
・LengthPointについて
松高子さんは松 高子
松高萌さんだったら松高 萌
と人間は分割するでしょう。これは「子」1文字の名前は存在しづらく、「萌」1文字の名前が存在しやすいことに起因しているのではないでしょうか。
という考えをモデル化したものです。
特徴量を用いて正しい場所で区切れているかそうでないかロジスティック回帰を行う
篠田麻里子を学習用にデータ処理するとこうなります。
Name,OrderPoint,LengthPoint,Answer
篠 田麻里子,0.121212121212121,0.205,0
篠田 麻里子,0.777253191702888,0.616753480620525,1
篠田麻 里子,0.126787212337516,0.246093120543235,0
篠田麻里 子,0.10023598578629,0,0
Answerは正しく区切れているかのbool
で、この処理を漢字学習データの一部(8000人弱)(以下回帰学習データ)に対して行い、rでプロットしたものが以下です。
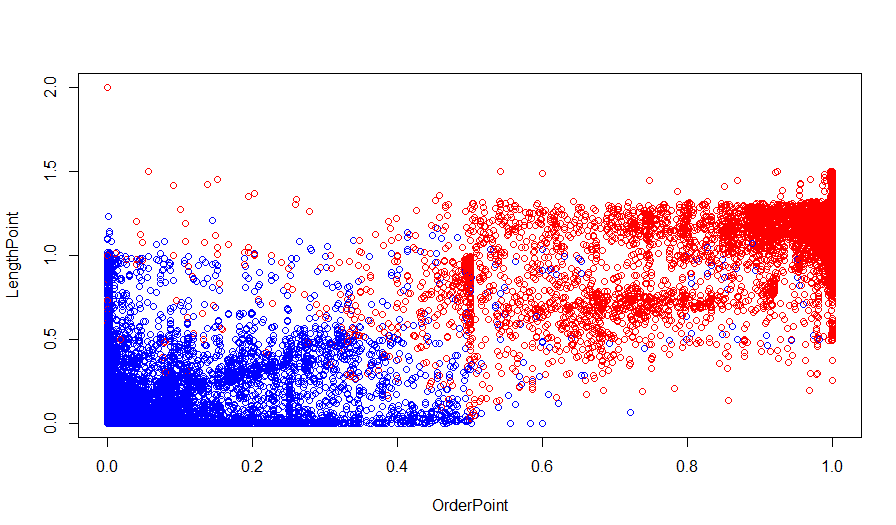
赤が正解、青が間違いです。まあまあうまくいっていると思いますので以下のようにロジスティック回帰をして
みたいな結果を得ます。
ここまでの説明でお分かりの方も多いと思いますが私はあんまり統計のことを理解できていないのでこの辺の解釈は今月中にします。
テストデータで評価
テストデータ
なでしこリーグに所属する選手200人弱+Jリーガー200人弱 = 394人分の人名
です。
漢字かな(カナ)交じりの名前は入れていますが、かな(カナ)のみの名前は入れていません。
評価手法
区切れるすべての個所で区切り、
作ったモデルにおいて値が最大になるものを真の名前と判定します。
ただし、漢字かな(カナ)交じりの名前は漢字とかなの区切れ目が姓名の区切れ目と判定します。
結果
正答:390
誤答:4
正答率:0.990
ワーイワーイ
ただし2文字目で切るだけでも正答率90出るのであんまり手放しには喜べませんが。。
結果の考察
なんかつらつら書いてたんですが実在する選手の名前についてあーだこーだいうのも悪趣味かなかなと思いはじめてきたんで後日アイマスのアイドルたちを姓名分割した結果をブログに書きます。
結果だけ言うと誤答2人/全体174人の正答率0.989でした。
まとめ
- 正答率0.990を誇る姓名分割プログラムが爆誕した
- ただ、ブログを書いている途中に使っている式に全く論理性がないことに気づき(LengthPointのとこ)凹む
- 実在の人名についてネット上であれこれ言うのはどうかと思い、結果の考察が次回に持ち越し
世界中誰でも姓名分離ができる夢のようなプログラムが使えるようにコンソールアプリを作っている(95%できている)ので、それも使い方記事と一緒に今度アップします。それでは。